We're continuing to explore different game algorithms using the simple game Color Walk. In the last post we took a deep dive into other heuristics that could be used instead of the obvious maximize-the-number-of-blocks-removed approach and found that the obvious choice is actually hard to beat. After looking at various heuristics, it's time we fill in some gaps in our exploration of algorithms by looking at a couple of fundamental graph algorithms: breadth-first search (BFS) and depth-first search (DFS). These algorithms are the two basic ways to search for something in a graph of nodes (or vertices) connected by edges, and a graph is exactly what we have when we draw out all possible move choices with each node representing a move and edges connecting sequential moves. We'll focus on BFS for this post.
Before We Begin, A Bug Fix
Before we start looking into BFS, we should make some small changes to the code to improve its performance. The implementation of the greedy look-ahead (GLA) algorithm that we've implemented a bug that is not affecting correctness, but it is slowing the search down considerably. Here is the code in its sub-optimal state:
this.greedyLookAhead = function() {
var max_control = _.max(controls, function(control) {
if (control.checkGameBoard(1, that.metric) === 0) {
return 0;
}
return greedyLookAheadN(2);
});
this.index = max_control.index;
}
function greedyLookAheadN(move) {
return _.max(_.map(controls, function(control) {
var matches = control.checkGameBoard(move, that.metric);
if (matches === 0 || move >= max_moves) {
return matches;
}
return greedyLookAheadN(move + 1);
}));
}Another improvement that can easily be made is to not search for blocks for a move that we already made on the preceding move, i.e. don't pick the same move twice in a row. The previously discussed if condition would end the search on the duplicate move when it's fixed, but only after searching for matches and finding no additional matches. We can skip the superfluous search by detecting when we're repeating the previous move. The fixes to the code involve passing the previous move and previous matches into greedyLookAheadN() so that they can be compared with the current move and matches, respectively:
this.greedyLookAhead = function() {
var max_control = _.max(controls, function(control) {
var matches = control.checkGameBoard(1, that.metric);
if (matches === 0) {
return 0;
}
return greedyLookAheadN(2, control, matches);
});
this.index = max_control.index;
}
function greedyLookAheadN(move, prev_control, prev_matches) {
return _.max(_.map(controls, function(control) {
if (control === prev_control) {
return 0;
}
var matches = control.checkGameBoard(move, that.metric);
if (matches === prev_matches || move >= max_moves) {
return matches;
}
return greedyLookAheadN(move + 1, control, matches);
}));
}Theoretical BFS
BFS is one of two fundamental ways to search a graph. We could be searching for a specific node value, searching for a maximum or minimum, or searching for something else based on node values. In our case, we're searching for the end-of-game condition where the board is cleared of blocks. The BFS algorithm is conceptually very simple: search the current node, then search that node's child nodes, then search those children's child nodes, and so on until we find what we're looking for.
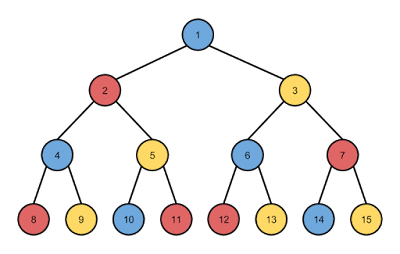
If we think of the graph as a tree with the current node at the root, then we're searching all nodes in the tree in order from those closest to the root to progressively deeper levels of the tree. To get a better visual picture of the process, let's assume we've arranged the move choices in Color Walk in the form of a tree, and we have three colors to pick from instead of five. Each move would consist of a choice between two colors, since we would never pick the same color twice in a row. A tree depicting three moves that were searched with BFS would look like this:
The move choices are blue, red, and yellow, and we just picked blue as our last move, so it is the root of the tree. Our choices for the next move are then red or yellow, and each level of the tree doubles in size compared to the level before it. The numbers in each node show the order that the nodes will be searched with BFS. The nice thing about this algorithm is that if we're searching for something specific, as we are for the end-of-game condition, then we know as soon as we find the first node with that condition that we can stop searching. That node resides at the level with the least number of moves to reach that state. We know this fact because we've searched each level of the tree in order from the level of the first move to the level of the first move found that completes the game. That means we've found an optimal solution.
Not everything is so nice, though. In reality this tree will be enormous. It grows exponentially, and we are dealing with a base of 4 instead of 2. If we assume the average game will have at least 30 moves, that means we'll have to search 430 = 260 nodes before finding the shortest sequence of moves to end the game. Even if we could represent each node with a single byte of data (which we most certainly can't), the tree would need over an exabyte of storage to hold it. If instead we generated the nodes we needed to search on the fly, and we assume it took a microsecond to generate and check each node (highly optimistic, especially for JavaScript), it would take 36,560 years to search the tree. Assuming the minimum number of moves is less doesn't help much. Reducing to 25 moves still results in almost 36 years of searching. None of this is feasible. The tree is just too big.
We need a way to cut this tree down to size, and to do it, we can use our old friend greedy. The idea is that the GLA algorithm works pretty well, and it's relatively fast. We can run with it for some number of moves at the beginning of the game to take some reasonably optimal path into the move tree. Then switch to the BFS algorithm to find the optimal sequence of moves from that point forward.
The issue that we need to resolve with this approach is when do we switch to the BFS algorithm? We don't want to switch too early, or it will still take a crazy long time to find the optimal path. We don't want to switch too late, or it will be practically useless to have switched algorithms at all. It's also difficult to tell when we're getting close to the end, at least with the information available at the time we're trying to decide. The best number of moves we've seen so far has varied from 25 to 40 over 100 random boards, so if we picked a fixed move number of, say, 20 to switch over to BFS, we could still be searching on the order of 420 nodes on some boards before finding the optimal path.
If instead we tried looking at how many blocks are left and created a threshold for when to switch, we would run into another problem. Sometimes one or more colors of blocks are not chosen for a long time, creating a large number of blocks of the same color that stay on the board until close to the end, when they are wiped out with a single move. At that point we would suddenly be too close to the end of the game for BFS to be useful. This behavior doesn't happen all of the time, either, compounding the problem of choosing an adequate threshold.
What we need is a way to try for BFS, but to bail on it if it's taking too long. We can start with GLA, and proceed to a safe number of moves, like 18. Then we can try using BFS for some reasonable number of nodes, and if we find the end-of-game condition, great. If we don't find it, then we'll run GLA for another move and try BFS again. The combined execution of both algorithms will be slower than running GLA by itself, but hopefully we'll find a more optimal sequence of moves. Now that we have a plan of action, we can start implementing the BFS algorithm. We'll start by adding it to the list of algorithms and adding its case to the switch statement of algorithms:
function Solver() {
// ...
this.init = function() {
// ...
$('#solver_type').change(function () {
switch (this.value) { case 'bfs':
that.solverType = that.bfsWithGla;
that.metric = areaCount;
break;
default:
that.solverType = that.roundRobin;
break;
}
// ...
});
}
// ...
this.bfsWithGla = function() {
if (moves < 18 || bfs() === false) this.greedyLookAhead();
}
}The if condition to use GLA is straightforward, and exactly like it was described: if there have been less than 18 moves or BFS fails, then run GLA for another move. The details of bfs() get more complex, so let's take a look at what a basic BFS algorithm looks like first and pick it apart:
function bfs() {
var nodes = addNodes(new Queue(), 1, null);
while (nodes.getLength() > 0) {
var node = nodes.dequeue();
if (node.control.checkGameBoard(node.depth, endOfGame)) {
return true;
}
nodes = addNodes(nodes, node.depth + 1, node.control);
}
return false;
}The use of a queue keeps the nodes in order as BFS searches through the move tree. The possible moves after the current move are added to the queue first, and then each of those moves are taken off the queue in order and inspected. If the end condition isn't found, each of those moves' child moves are added to the queue, in order. This process ends up with each level of moves being added to the queue in succession until either the search runs into the end condition or the entire tree has been searched.
Practical BFS
The BFS algorithm as it stands has some problems, though. First, it doesn't do anything to limit the length of the search, so if we switch to BFS on the 18th move, many boards will end up searching effectively forever. We need to limit the search somehow. Second, we can do better than simply returning true when we find the end condition. Since we know what moves produced the ending, we can simply do those moves right away and be done. Last, we need some way for each node to keep track of which moves led to that particular node. It's clear from the code that a node will have information about which control was used for its move and its depth in the tree, but not a full record of the moves taken to get to that node. We need that information attached to the nodes, and we can do it by maintaining an array of move numbers, called markers, that we'll discuss in a moment. First, here is what the augmented bfs() code looks like:
function bfs() {
var nodes = addNodes(new Queue(), 1, null);
var still_adding_nodes = true;
while (nodes.getLength() > 0) {
var node = nodes.dequeue();
markers = node.markers;
if (node.control.checkGameBoard(node.depth, endOfGame)) {
doMarkedMoves();
return true;
}
if (still_adding_nodes) {
nodes = addNodes(nodes, node.depth + 1, node.control);
still_adding_nodes = nodes.getLength() < 16384;
}
}
return false;
}A threshold of 16384 allows for about 7 levels of moves to be searched. The nice thing about limiting the search in this way is that if we decide to trim out some move choices before adding them to the queue, the algorithm will automatically search deeper into the tree in the same amount of search time. Limiting the search by level would require a change to the threshold if we wanted to search deeper, and it would have to search the entire next level. Remember that level size grows exponentially. By limiting the queue size, we could decide to partially search the last search level if it was too big. Alternatively, we could limit the search by run time and get the added benefit that if we could improve the checkGameBoard() performance, the algorithm would automatically search deeper as well.
The second addition to the code, doMarkedMoves() is pretty self-explanatory at this level. We'll get into the details if it after describing the markers array for keeping track of moves for each node.
The markers array is basically the marked property from each Block object consolidated into one array for easy, compact copying to each node in the move tree. (See part 4 for how the marked property works.) We could copy the entire blocks array for each node, but the majority of the data in a block never changes during a search. Only the marked property would change, so we can pull it out and make it its own markers array that mirrors the blocks array. To make this change, we can add markers at the top level:
function colorWalk() {
var blocks = [];
var clusters = [];
var markers = [];
// ... function addNodes(nodes, depth, prev_control) {
var markers_dup = markers.slice();
_.each(controls, function (control) {
if (control !== prev_control) {
nodes.enqueue({markers: markers_dup, depth: depth, control: control});
}
});
return nodes;
}Now that we know how to add and remove nodes from the queue, let's look at how we can use the markers array to find the sequence of moves taken to clear the board when the end-of-game condition is found:
function doMarkedMoves() {
var move_sequence = markers.slice();
var move = 1;
var i = _.indexOf(move_sequence, move);
while (i > 0) {
var control = _.findWhere(controls, {color: blocks[i].color});
control.updateGameBoard();
move += 1;
i = _.indexOf(move_sequence, move);
}
}Performant BFS
At this point the code works, but there's a problem. The first couple of iterations seem to run okay, about ten seconds each on my machine, but each iteration quickly starts taking longer. It isn't too many iterations in before each one is taking upwards of five minutes to complete. Not long after that, the program crashes with an out-of-memory error. We seem to have a memory leak, and it obviously has something to do with creating tens of thousands of node objects. Somehow the garbage collector is not reclaiming all of that memory.
After doing some research and much pondering, I think the problem stems from having a pointer to an object outside of a scope (the markers array) and more pointers to the same object at certain times in multiple levels of nested scope (in bfs() and Queue()). The GC can't tell when nodes have no more pointers to them, so their memory is not freed, creating the memory leak. The way to fix this leak is to explicitly set the pointers to null when they are no longer used:
function bfs() {
var nodes = addNodes(new Queue(), 1, null);
var still_adding_nodes = true;
while (nodes.getLength() > 0) {
var node = nodes.dequeue();
markers = null;
markers = node.markers;
if (node.control.checkGameBoard(node.depth, endOfGame)) {
doMarkedMoves();
return true;
}
if (still_adding_nodes) {
nodes = addNodes(nodes, node.depth + 1, node.control);
still_adding_nodes = nodes.getLength() < 16384;
}
node.markers = null;
}
return false;
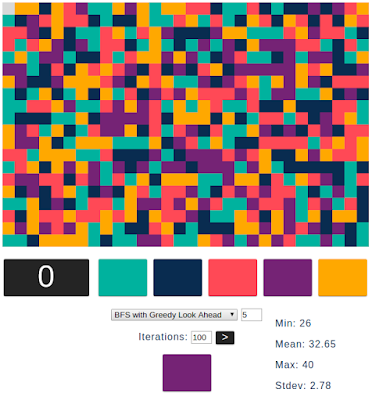
}The completed run of 100 iterations, using a GLA depth of 5, came up with these results:
The results look promising, but let's compare it to a selection of the other algorithms:
| Algorithm | Min | Mean | Max | Stdev |
|---|---|---|---|---|
| RR with Skipping | 37 | 46.9 | 59 | 4.1 |
| Random with Skipping | 43 | 53.1 | 64 | 4.5 |
| Greedy | 31 | 39.8 | 48 | 3.5 |
| Greedy Look-Ahead-2 | 28 | 37.0 | 45 | 3.1 |
| Greedy Look-Ahead-5 | 25 | 33.1 | 41 | 2.8 |
| Max Perimeter | 29 | 37.4 | 44 | 3.2 |
| Max Perimeter Look-Ahead-2 | 27 | 35.0 | 44 | 2.8 |
| Perimeter-Area Hybrid | 31 | 39.0 | 49 | 3.8 |
| Deep-Path | 51 | 74.8 | 104 | 9.4 |
| Path-Area Hybrid | 35 | 44.2 | 54 | 3.5 |
| Path-Area Hybrid Look-Ahead-4 | 32 | 38.7 | 45 | 2.7 |
| BFS with Greedy Look-Ahead-5 | 26 | 32.7 | 40 | 2.8 |
The BFS algorithm just barely squeaks out a victory over the GLA-5 algorithm on average and on the maximum. It's one move longer than GLA-5 on the minimum. This slight win came at a cost of significantly reduced speed, however, as the BFS algorithm runs considerably slower than GLA-5. It is, after all, running GLA-5 for most of each iteration, and only finishing off with BFS to find the end-of-game condition.
Even if we didn't make significant improvements with the BFS algorithm, we did learn a number of things. We learned how to implement a BFS algorithm using a queue, and that the basic idea is fairly simple. Theoretically, BFS will give an optimal solution to the problem of finding a minimum sequence of moves for Color Walk, but the exponential growth of the move tree presents an insurmountable problem for a pure BFS algorithm in practice. To make BFS tractable, we need to start with a good, fast algorithm like GLA to cut down the tree size before switching to BFS. Finally, using BFS to augment GLA can make incremental improvements to the performance, but it's not a slam dunk because of significant costs in run time. Next time we'll explore the other fundamental graph search algorithm, depth-first search, and see what problems we need to overcome there.
Article Index
Part 1: Introduction & Setup
Part 2: Tooling & Round-Robin
Part 3: Random & Skipping
Part 4: The Greedy Algorithm
Part 5: Greedy Look Ahead
Part 6: Heuristics & Hybrids
Part 7: Breadth-First Search
Part 8: Depth-First Search
Part 9: Dijkstra's Algorithm
Part 10: Dijkstra's Hybrids
Part 11: Priority Queues
Part 12: Summary